Adjunctions and data migration

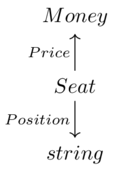
Pulling back data along a functor(4)
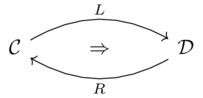
Functor pullback(1)

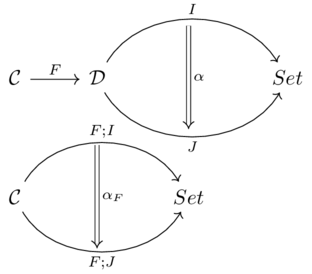
The pullback of functor \(\mathcal{D}\xrightarrow{I}\mathbf{Set}\) along functor \(\mathcal{C}\xrightarrow{F}\mathcal{D}\)

  • The composite functor \(\mathcal{C}\xrightarrow{F;I}\mathbf{Set}\)

  • Given a natural transformation \(I \overset{\alpha}\Rightarrow J\), there is a natural transformation \(\alpha_F\) whose components (morphisms in Set from \((F;I)(c)\) to \((F;J)(c)\), for any \(c \in \mathcal{C}\) are given by: \((\alpha_F)_c := \alpha_{F(c)}\)

DDS pullback(1)

  • Pulling back data along a functor

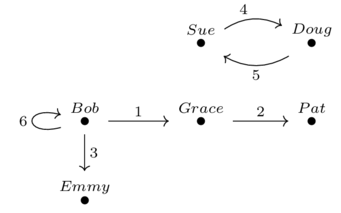
  • We’ll migrate data between the graph-indexing schema Gr and the loop schema, called DDS (for discrete-dynamical system).

  • We’ll write down an example instance \(\mathbf{DDS}\xrightarrow{I}\mathbf{Set}\)

State Next
1 4
2 4
3 5
4 5
5 5
6 7
7 6

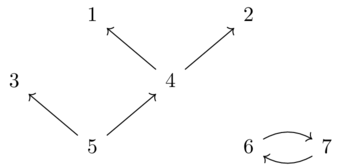
  • We want to convert this state information into a graph that will let us visualize our machine.

  • Use the following functor \(F\):

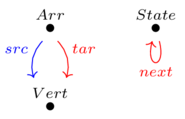
    • src is sent to identity

    • Can now generate a graph using the composite functor \(\mathbf{Gr}\xrightarrow{F}\mathbf{DDS}\xrightarrow{I}\mathbf{Set}\)

Arr src tar
1 1 4
2 2 4
3 3 5
4 4 5
5 5 5
6 6 7
7 7 6

\(Vert = \bar{7}\)

  • We can now draw the graph:

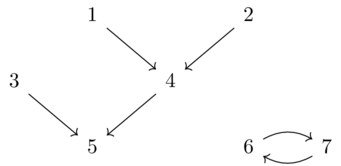
  • This procecure can be called “pulling back data along a functor". We pulled back data \(I\) along functor \(F\) (via functor composition).

Linked by

Exercise 3-67(2)

Consider the functor \(\mathbf{Gr}\xrightarrow{G}\mathbf{DDS}\) given by sending src to next and tar to id on State. Migrate the same data as in Example 3.65 and draw the corresponding graph.NOCARD

Solution(1)
Arr src tar
1 4 1
2 4 2
3 5 3
4 5 4
5 5 5
6 7 6
7 6 7

Adjunctions(6)
Adjoint functor(1)

A functor \(\mathcal{C}\xrightarrow{L}\mathcal{D}\) is left adjoint to a functor \(\mathcal{D}\xrightarrow{R}\mathcal{C}\)

  • For any \(c \in C\) and \(d \in D\), there is an isomorphism of hom-sets: \(\alpha_{c,d}: \mathcal{C}(c,R(d)) \xrightarrow{\cong} \mathcal{D}(L(c),d)\) that is natural in c and d.

  • Given a morphism \(c \rightarrow{f} R(d)\) in \(\mathcal{C}\), its image \(g:=\alpha_{c,d}(f)\) is called its mate (and vice-versa)

  • To denote the adjunction we write \(L \dashv R\) or

Linked by

Galois connections are adjoint(1)

Galois connections between preorders are the same as adjunctions between the corresponding categories.

Currying(1)

The adjunction called currying says \(\mathbf{Set}(A \times B,C)\cong \mathbf{Set}(A,C^B)\)

Linked by

Adjoint examples(1)

Examples of adjunctions

  1. Free constructions: given a set you get a free groupmonoidring/vector space/etc. - each of these is a left adjoint. The corresponding right adjoint throws away the algebraic structure.

  2. Given a graph you get a free preorder or a free category, the corresponding right adjoint is the underlying graph of a preorder/category.

  3. Discrete things: given any set you get a discrete preordergraphmetric spacecategorytopological space/etc.; each of these is a left adjoint and the corresponding right adjoint again recovers the set.

  4. Codiscrete things: given any set you get a codiscrete preorder, complete graph, codiscrete category, category, etc.; each of these is a right adjoint and the left adjoint gives the underlying set.

  5. Given a group, you can quotient by its commutator subgroup to get an abelian group; this is a left adjoint. The right adjoint is the inclusion of abelian groups into Grp

Exercise 3-73(2)

Currying was an adjunction between functors in Set, but the example only discussed what the functors did to objects.

  1. Given a morphism \(X \xrightarrow{f}Y\), what morphism should \(X \times B \xrightarrow{-\times B}Y\times B\) return?

  2. Given a morphism \(X \xrightarrow{f}Y\), what morphism should \(X^ B \xrightarrow{(-)^B}Y^B\) return?

  3. Consider \(\mathbb{N}\times \mathbb{N}\xrightarrow{+}\mathbb{N}\). Currying \(+\), we get a certain function \(\mathbb{N}\xrightarrow{p}\mathbb{N}^\mathbb{N}\). What is \(p(3)\)?

Solution(1)

  1. This morphism maps \((x,b)\mapsto (f(x),b)\)

  2. This morphism takes in a function \(B \xrightarrow{bx} X\) and composes with f to give \(B \xrightarrow{bx;f} Y\)

  3. It takes a number and returns a function which adds three to that number.

Left and right pushforward functors(2)

Given \(\mathcal{C}\xrightarrow{F}\mathcal{D}\), the data migration functor \(\Delta_F\) turns \(\mathcal{D}\) instances to \(\mathcal{C}\) instances. This functor has both a left and right adjoint:

Migration Functor Pronounced Reminiscent of Database idea
\(\Delta\) Delta Duplicate or destroy Duplicate or destroy tables or columns
\(\Sigma\) Sigma Sum Union (sum up) data
\(\Pi\) Pi Product Pair and query data
Plane tickets(1)

  • Consider a functor which discards the distinction between Economy and First Class seats in an airplane.

  • The \(\Delta\) functor is uninteresting - it will copy the rows for Seat into both Economy and First class.

  • The functor \(\Pi\) puts into each airline seat only seats which are in both the Economy and First Class tables with the same price and position.

  • The functor \(\Sigma\) puts all Economy and First Class seats into the Seat table and discards the information of from which table they came from.

Single set summaries of databases(5)
Emails(1)

  • Consider the schema \(\mathfrak{g} := \boxed{\overset{Email}\bullet \overset{sentBy}{\underset{receivedBy}{\rightrightarrows}} \overset{Address}\bullet}\)

  • And an example instance: \(\mathfrak{g}\xrightarrow{I}\mathbf{Set}\)

Email SentBy ReceivedBy
1 Bob Grace
2 Grace Pat
3 Bob Emmy
4 Sue Doug
5 Doug Sue
6 Bob Bob

  • Data migration functors \(\Sigma_!,\Pi_!\) go from \(\mathcal{C}\) Inst to 1-Inst, but we showed that 1-Inst is equivalent to Set in Example 3.53.

  • \(\Sigma_!\) tells us the mailing groups, the "connected components" in \(I\):

1
Bob-Grace-Pat-Emmy
Sue-Doug

  • \(\Pi_!\) tells us the emails that were sent from a person to themselves

    1
    \(Em_6\) (Bob)

Linked by

Exercise 3-76(2)

For any category \(\mathcal{C}\) there is exactly one functor to the category 1, let’s call it \(!\) Where does it send each object and each morphism?

Solution(1)

There is only one object to send each object to and only one morphism to send each morphism to. Because everything in the target is equal to everything else, all functor constraints are trivially satisfied.

Exercise 3-78(2)

Draw the instance \(I\) in Example 3.77 as a graph.NOCARD

Solution(1)